gl-reactを使ってGLSLでお絵描きをしてみます。
以下と同じようなGLSLの練習メモです。
直交座標の三角関数
練習がてらsin、cos、tanを書いてみましょう。
座標をuv(0~1, 0~1)をxy(0~2π, -1~1)に変えて式との差を見ます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
precision highp float; varying vec2 uv; void main() { vec4 c = vec4(vec3(0.0), 1.0); float x = 2.0 * 3.14159 * uv.x; // 0 < x < 2pi float y = uv.y * 2.0 - 1.0; //-1 < y < 1 float v1 = sin(x); float v2 = cos(x); float v3 = tan(x); float diff1 = 1.0 - abs(y-v1)/2.0; float diff2 = 1.0 - abs(y-v2)/2.0; float diff3 = 1.0 - abs(y-v3)/2.0; c.x += pow(diff1, 100.0); c.y += pow(diff2, 100.0); c.z += pow(diff3, 100.0); gl_FragColor = c; } |
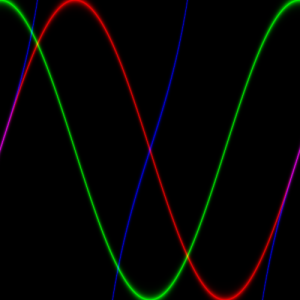
diffの最大値を1.0にして累乗しまくればいいかと思いましたが、計算的にどうやってもぼやけるのと負荷が気になるところ。
step関数を使って書き直します。
|
1 2 3 4 5 6 7 8 |
//0 < diff < 2 float diff1 = abs(y-v1); float diff2 = abs(y-v2); float diff3 = abs(y-v3); c.x += step(diff1,0.01); c.y += step(diff2,0.01); c.z += step(diff3,0.01); |
step(th, x)なのでdiffが閾値で0.01>=diffなら1.0、小さければ0.0です。
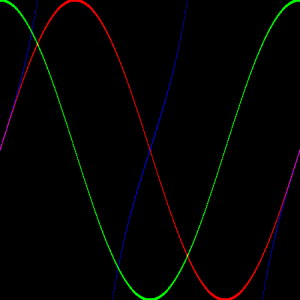
式次第では面白いものもできるかもしれませんが、そんなに数学マニアでもないので回転対称な図形を書きやすい極座標系を用います。
極座標系
座標を角度と距離で表します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
precision highp float; varying vec2 uv; void main() { vec2 p = uv - vec2(0.5); vec4 c = vec4(vec3(0.0), 1.0); float a = atan(p.y, p.x); float r = length(p)*2.0; float f = sin(4.0*a); c.x = step(abs(r-abs(f)),0.01); gl_FragColor = c; } |
適当な周期関数と比較することで回転対称な図形になります。
計算的に中央が疎になるのはちょっと補正したほうがよさそうな気もする。

単純な塗り絵ならこれだけでもそれっぽい画像になります。
|
1 2 3 |
c.x = step(r, f); c.y = step(r, -f); c.z = step(r,abs(f)); |

この辺の周期関数を適当に弄れば花っぽいものも作れます。
試しにコスモスを作ってみましょう。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
void main() { vec2 p = uv - vec2(0.5); vec3 c = vec3(0.0); float a = atan(p.y, p.x); float r = length(p)*2.0; float f1 = sin(4.0*a) + 0.125*sin(12.0*a); float f2 = sin(4.0*a); float f3 = sin(4.0*a+3.1415/2.0); c = vec3(0.9,0.4,0.6) * step(r, abs(f1)); c = step(r*5.0, abs(f2)+abs(f3))==1.0 ? vec3(0.9,0.8,0.0) : c; gl_FragColor = vec4(c, 1.0); } |

色々できそうで面白いけど実用的ではないかな。