golangで乱数を扱うならmath/randパッケージがありますが、そのまま使っていいものかわからなかったので色々見て確認してみます。
ソース:math/rand/rng.go
Wikipedia:線形合同法、Lagged Fibonacci 法、メルセンヌ・ツイスタ
線形合同法
いきなり横道にそれますが乱数を使う時に「それって線形合同法じゃないよね?」といわれるような風潮があります。
この辺の理由も直感的に分かりにくかったので簡単に書いてみます。
A、B(C)、Mは英語の方のwikiを参考にしました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
//LCG : Linear congruential generators type LCG struct { a, b, m, x int } func (l *LCG) get() int { l.x = (l.a*l.x + l.b) % l.m return l.x } //get with mask bit func (l *LCG) getm() int { l.x = (l.a*l.x + l.b) & l.m return l.x } func doLcg() { r1 := &LCG{22695477, 1, (1 << 32) - 1, 1} //Borland C/C++ r2 := &LCG{1103515245, 12345, (1 << 31) - 1, 1} //glibc println("--- LCG 1 ---") fmt.Printf("%10d\n%10d\n%10d\n%10d\n", r1.getm(), r1.getm(), r1.getm(), r1.getm()) println("--- LCG 2 ---") fmt.Printf("%10d\n%10d\n%10d\n%10d\n", r2.getm(), r2.getm(), r2.getm(), r2.getm()) /* --- LCG 1 --- 22695478 2156045615 2867233980 71484141 --- LCG 2 --- 1103527590 377401575 662824084 1147902781 */ } |
2nの剰余は2n-1のマスクビットで得られるのでそっちを使います。
よく見る偶数と奇数が交互にくるってやつでしょうか。奇数*X+奇数の下位ビットをマスクしているので最下位ビットが交互に来るのはしょうがない。
実際には全てのビットを使うわけではないですが、こういった周期性が問題になるようです。
2の累乗を最大値にしてプロットしてみると周期性の問題がよくわかります。
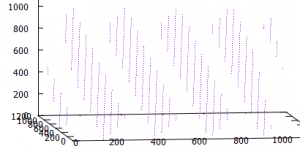
GOの乱数
本筋に戻ってrandのソースを見ていきます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
func seedrand(x int32) int32 { const ( A = 48271 Q = 44488 R = 3399 ) hi := x / Q lo := x % Q x = A*lo - R*hi if x < 0 { x += int32max } return x } |
231 - 1 = 48271 * 44488 + 3399 で Q = M / 48271、R = M % 48271。
Seed()を見ると607個のスタックに詰めつつ、273離れたインデックス2つ(tap,feed)を用意している。
そして乱数を出す部分ではtap,feedをずらしてx := rng.vec[rng.feed] + rng.vec[rng.tap]を返している。
これはラグ付フィボナッチ法のようです。
(273,607)の組み合わせは有名なものみたいなのでそこから調べればよかった。
ついでにシード値の設定は以下のようなものがある。
|
1 2 3 4 5 6 7 |
//timeを使う rand.Seed(time.Now().UnixNano()) //crypto/rand(プログラムとは関係のない乱数)を使う //import cryptorand "crypto/rand" seed, _ := cryptorand.Int(cryptorand.Reader, big.NewInt(math.MaxInt64)) rand.Seed(seed.Int64()) |
メルセンヌ・ツイスタ
math/randでは特に問題は起きなかったけど乱数作るならとりあえずメルセンヌツイスタじゃないかという風潮もある。
GitHubでライブラリを探すとcpmech/goslとseehuhn/mt19937がありました。
必要があるならこれらを使ってみてもいいと思います。
