前回トゥーン化シェーダーを試したときにガウシアンフィルタを使いました。
使った後で、これって本当にあってるんだっけと思い始めて少し深堀り。
ガウシアンフィルタ
平滑化、ぼかしを行うフィルタです。
ガウシアンフィルタというと、まずこの手の行列を思い出します。
合計が1となる、周辺画素への重みづけを行ったマスクです。

ガウス分布に従うということで以下の式も紹介される。
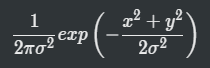
これはガウス分布(正規分布)の式を2次元にして平均を0とすると同じ。
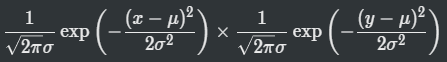
最初の行列ってこの式に従ってるんだろうかという話です。
パスカルの三角形
フィルタの行列を考える前に、パスカルの三角形という図を思い出します。
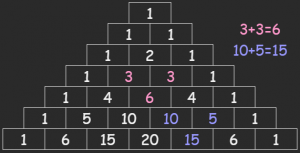
こんな感じで両辺を1、中央は上2つの合計になる三角形です。
格段の数字は (x+y)n を展開したときの各項の係数に等しくなります。
![]()
最初に見た行列はこのパスカルの三角形の奇数段を掛けることで導けます。
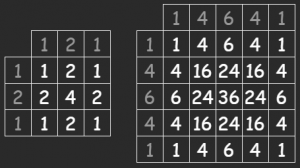
それでこれは本当にガウシアンフィルタ何だろうか。
確認
適当に javascript を書いてみる。
数式に注目点を 0 とした座標を渡す。分散は適当に行列に合わせた。
合計を1にすることを忘れずに。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
const g = (x, y, s) => Math.exp(-(x * x + y * y) / (2 * s * s)) / (2 * Math.PI * s * s); let sum = 0; let mat = [ [0, 0, 0], [0, 0, 0], [0, 0, 0], ]; for (let i = 0; i < 9; i++) { mat[Math.floor(i / 3)][i % 3] = g(Math.floor(i / 3) - 1, (i % 3) - 1, .85); sum += mat[Math.floor(i / 3)][i % 3]; } for (let i = 0; i < 9; i++) mat[Math.floor(i / 3)][i % 3] /= sum; console.log(mat); |
3×3 行列の 3 要素を比較してみるとほぼ同じになる。
|
1 2 3 4 |
| g() / σ=0.85 1/16=0.0625 | 0.06256912272348984 2/16=0.125 | 0.12499996179751512 4/16=0.25 | 0.24972366191598003 |
もう少し突き詰めてみると分散 σ=.8493218003 でこうなった。
![]()
5x5 の場合は σ=1.0483 付近でほぼ同じになります。
ちゃんとガウシアンフィルタだった。ヨシ!
この分散値がフィルタとして良いのかどうかは不明ですが、離散に当てはめてるだけだしそんなに気にしなくてもいい気がする。