前々回、前回と直線を書いた※ので、より使いやすくするために線分を書けるようにします。
※前々回の失敗版は実は線分でした。
線分の判定
処理する点 p と線分の始点 s、終点 e の内積を見ます。
ベクトル se に対しての角度が90度を超えると内積同士の積が + になるので、内積の積が - の場合にのみ判定をすればいいです。
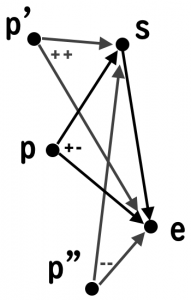
処理を 3-4 行目を追加しました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
void line(vec2 s,vec2 e){ vec2 p=gl_FragCoord.xy/resolution; vec2 se=e-s,ps=s-p,pe=e-p; if(dot(ps,se)*dot(pe,se)>0.)return; if(s.x!=e.x){ float a=(e-s).y/(e-s).x; float d=abs(a*p.x-p.y-a*s.x+s.y)/sqrt(a*a+1.); cs=max(pow(3e-3/(d+1e-6),3.),cs); }else{ float d=abs(p.x-s.x); cs=max(pow(3e-3/(d+1e-6),3.),cs); } } |
適当に線分を引いてみましょう。
|
1 2 3 4 5 6 7 8 9 |
void thunder(vec2 s,vec2 e){ line(vec2(.1,.7),vec2(.9,.7)); line(vec2(.2,.5),vec2(.8,.5)); line(vec2(.5,.4),vec2(.5,.8)); line(vec2(.4,.4),vec2(.2,.8)); line(vec2(.6,.4),vec2(.8,.8)); line(vec2(.5,.6),vec2(.7,.6)); line(vec2(.4,.5),vec2(.4,.7)); } |
 |
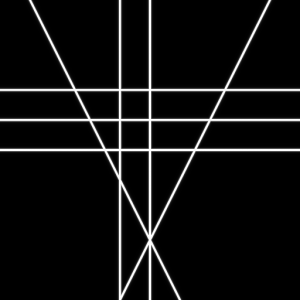 |
ちゃんと線分が書けるようになりました。