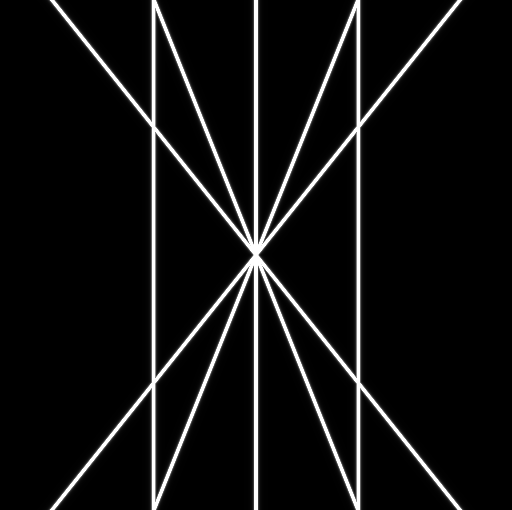
前回線を引くときに頭をよぎった「数式が書けるなら y=ax+c の形に点 p を当てはめるだけでいいんじゃない?」を少し考えます。
※もちろんよくないです。
ついでに縦線も引けるように。
線の式への当てはめ
プログラムにするとこんな感じ。太さは適当に弄ってます。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
void line(vec2 s,vec2 e){ vec2 p=gl_FragCoord.xy/resolution; vec2 l=e-s; float a=l.y/l.x; //float d=abs(a*p.x-p.y-a*s.x+s.y)/sqrt(a*a+1.); float y=a*p.x-a*s.x+s.y; float d=abs(p.y-y); cs=max(pow(13e-3/(d+1e-6),3.),cs); } |
 |
 |
何か今回の書き方だと線の太さがバラバラな気がしますね。
傾きを変えてみると分かりやすいです。
 |
 |
x 毎に y の値で判定しているため、傾きが大きいと判定がシビアになります。
ちゃんと公式を使いましょう。
縦線を引く
前回も今回も縦線(傾き∞)の線を引けません。
なんとかきれいに対応できないか考えましたが無理そうなので、普通に場合分けで対応することにします。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
precision highp float; uniform vec2 resolution; vec3 co=vec3(1,1,1); float cs=0.; void line(vec2 s,vec2 e){ vec2 p=gl_FragCoord.xy/resolution; if(s.x!=e.x){ float a=(e-s).y/(e-s).x; float d=abs(a*p.x-p.y-a*s.x+s.y)/sqrt(a*a+1.); cs=max(pow(3e-3/(d+1e-6),3.),cs); }else{ float d=abs(p.x-s.x); cs=max(pow(3e-3/(d+1e-6),3.),cs); } } void thunder(vec2 s,vec2 e){ //line(s,e); line(vec2(.3,1.),vec2(.7,0.)); line(vec2(.7,1.),vec2(.3,0.)); line(vec2(.1,1.),vec2(.9,0.)); line(vec2(.9,1.),vec2(.1,0.)); line(vec2(.3,1.),vec2(.3,0.)); line(vec2(.5,1.),vec2(.5,0.)); line(vec2(.7,1.),vec2(.7,0.)); } void main(void){ vec2 p=gl_FragCoord.xy/resolution; thunder(vec2(.55,1.),vec2(.45,0.)); gl_FragColor=vec4(co*cs,1.); } |
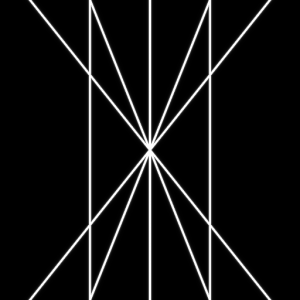
綺麗に縦線を引けました。
(サンプルは錯視によって若干膨らんで見えますが…)
綺麗に線を引けるようになったので雷の描画に戻ります。