GLSLで円周率の定義方法と用いるfloatの精度についての覚書きです。
別に知らなくても問題ないので大抵は気にしなくていいやつです。
円周率πの定義
GLSLでは円周率が定義されていないので自分で用意する必要があります。
#define PI 3.14なんかもわかりやすくていいんですが、ちゃんと定義したいなら逆三角関数を使うと簡単に定義できます。
-
acos(-1.) -
asin(1.)*2. -
atan(1.)*4.
cos(π)=-1, sin(π/2)=1, tan(π/4)=1を逆三角関数でπを算出してます。
以下を差し込むとわかりますが、どれを使っても同じです
|
1 2 3 4 |
//後で触れますが、この比較はあまりよくないです if(acos(-1.)==asin(1.)*2. && acos(-1.)==atan(1.)*4.){ gl_FragColor=vec4(1.); } |
シンプルで文字数も少ないacosがいいと思うんですがatanを使ってるのをよく見かけます。まぁ好きな奴で。
一緒にτも定義しておくと便利です。
|
1 2 |
float pi = acos(-1.); float tau = pi*2.; |
【短く書きたいときの参考】18文字で書けるπ精度
float 浮動小数点の比較について
適当に数値を使った処理をしていると時折気になる動作をしていたので、ちゃんと考えてみる。
GLSLの精度は?
まずprecision highp floatの場合、精度はどうなるのか。
OpenGLの定義を見てみるとこんな感じです。
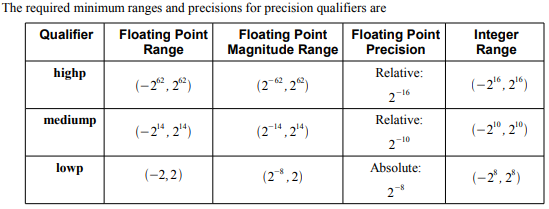
最低限これを満たすってことだろうけどわかりにくい。
WebGL2.0の元になるES 3.0ではこのように書かれていました。
The precision of highp floating-point variables is defined by the IEEE 754 standard for 32-bit floatingpoint numbers. (参照元)
わかりやすい。通常の単精度浮動小数点数ですね。
ただ定義ではこうなっていても環境(実装)次第で変わるので、以下のテストコードなんかも参考程度にしかならないと思います。
同値比較の失敗
一般に浮動小数点数同士の同値比較はNGです。
試しに円周率ベースで実験。
|
1 2 3 4 5 |
void main() { gl_FragColor=vec4(1,0,0,1); if(3.14159263==3.14159286){gl_FragColor=vec4(0);}//true if(3.14159263==3.14159262){gl_FragColor=vec4(1);}//false } |
大分違和感のある結果になります。
計算もなく数値比較するだけでこれくらいの誤差が出てきます。
他言語だとfalse positive(OKなのにNG)な判定が多い気がするけど、GLSLではfalse negative(NGなのにOK)な判定になる気がします。
つまり普通に比較しちゃってもある程度は想定通り動きます。
本当はどうするのがいいか
float同士の比較をするなら差分が0に近いかを見る必要があります。
|
1 2 3 4 5 6 7 8 9 |
float epsilon = 0.00001; bool feq(float a,float b){ return abs(a-b)<epsilon; } void main() { if(feq(acos(-1.), asin(1.)*2.)){ gl_FragColor = vec4(1,0,0,1); } } |
この比較する数値は一般的にε(Epsilon)として、これより小さな値は誤差ということにしています。
単精度なので10進数だと大体6, 7桁くらいの精度のはずです。ε=1e-5くらいでいいんじゃないでしょうか。
相対で精度2-16が保証されていますがそっちで計算するのも違う気がする。
そもそも小数点何桁まで処理できるの?
どこまで小さな数を使えるんだろうという疑問がわいた。
試しに以下のように書いていって、どこまで比較可能か確かめました。
|
1 2 3 4 5 6 7 8 9 |
void main() { gl_FragColor=vec4(1,0,0,1); if(0.<1e-37){ //true gl_FragColor=vec4(1.); } if(0.<1e-38){ //false gl_FragColor=vec4(0.); } } |
1e-37まで使えるようですね。
2の累乗で境界を探してみよう。
|
1 2 3 4 5 6 7 8 9 |
void main() { gl_FragColor=vec4(1,0,0,1); if(0.<pow(2.,-149.)){ //true gl_FragColor=vec4(1.); } if(0.<pow(2.,-150.)){ //false gl_FragColor=vec4(0.); } } |
単精度浮動小数点数(IEEE 754)の限界値まで処理出来る(使い道は相当限られるだろうけど)。
πの話に戻ると以下のGLSLの結果は赤。つまりもう差が0ですね。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
float epsilon = 1e-37; bool feq(float a,float b){ return abs(a-b)<epsilon; } void main() { float c = acos(-1.); float s = asin(1.)*2.; float t = atan(1.)*4.; if(feq(c, s) && feq(c, t)){ gl_FragColor=vec4(1,0,0,1); } } |
この式でepsilonに2の累乗を使うと 2-126 まで赤で 2-127以降は黒でした。
